Triangles

Complex 3D scenes are made entirely of triangles. Our graphics cards know nothing of quadrilaterals, pentagons, hexagons, or any other polygon. They don't have to, because any polygon can be decomposed into triangles. Consider these regular polygons:

When viewing them in wireframe, we see that the square is just two triangles, the pentagon is three triangles, and the hexagon is four:

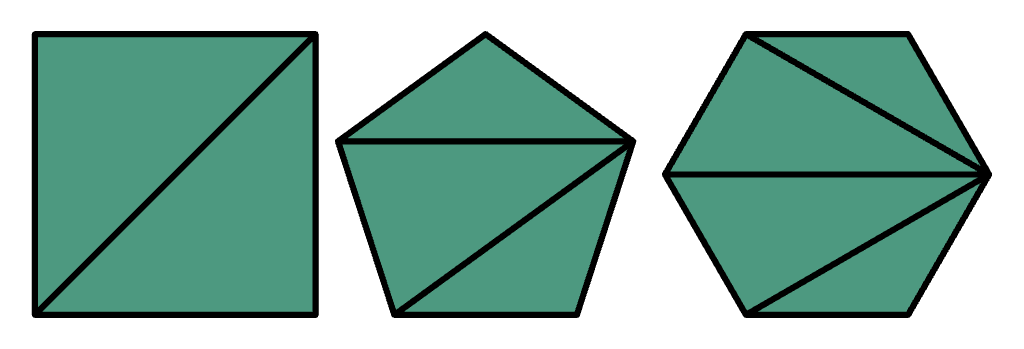
These polygons are regular, but any polygon can be decomposed into triangles, no matter its concavity, convexity, or irregularity. In fact, there are often multiple ways to break up a polygon.

Even complex, non-planar 3D shapes can be decomposed into a quilt of just triangles. Consider this cylinder:

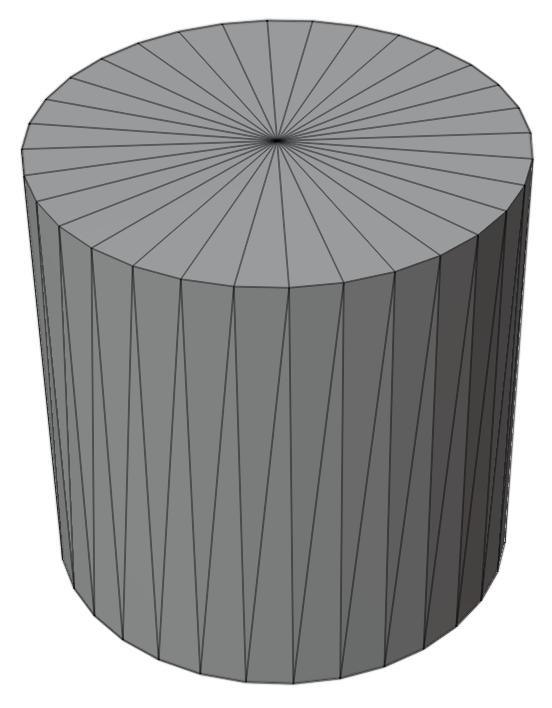
If we need to render high-quality curved surfaces, we'll likely need many small triangles. This renderer produces an approximation of a sphere by subdividing a tetrahedron's four equilateral triangles into smaller triangles and pushing out the new vertices to the sphere's surface:

Increase the quality of the approximation by increasing the number of subdivisions. Rotate the sphere with the mouse.

We limit graphics program to just triangles because triangles have several advantages over other polygons:

• Triangles have been studied for centuries, and their mathematical properties are well-known and relatively simple compared to other polygons.
• A triangle is necessarily planar, whereas a list of four or more vertices may not form a flat polygon.
• Graphics cards have circuitry optimized for processing triangles.

In this chapter we explore how to form models out of triangles and render them in a 3D scene. By its end, you'll be able to answer the following questions:

• What triangular geometric primitives does WebGL support and how do these primitives affect the interpretation of the vertex buffer?
• How can vertices be shared amongst several triangles without repeating them in the vertex buffer?
• How are a triangle's fragments filled in if its vertices have different property values?
• What mathematical machinery is typically used to position, orient, and shape a model on the fly—at render time rather than at modeling time?

These initial chapters focus on describing a model's shape. As we move into the third dimension, we will naturally feel a strong desire to add illumination and shading to communicate a shape's depth and orientation. However, we're not yet ready. Shape comes first.