Spotlight

Point lights and directional lights emit light in every direction. What if we want to render a light under a lamp shade or on a tower during a prison escape? We need a spotlight that emits a cone of light.

Three pieces of information are needed to model a spotlight:

• Where is it? This is the light position that we've already seen with point lights.
• In what direction is it aimed? This the spot direction.
• How wide is its aperture? This is the spot angle.

A fragment is illuminated if it falls within the spotlight's cone of focus. In this figure, point A is inside the cone and point B is outside:

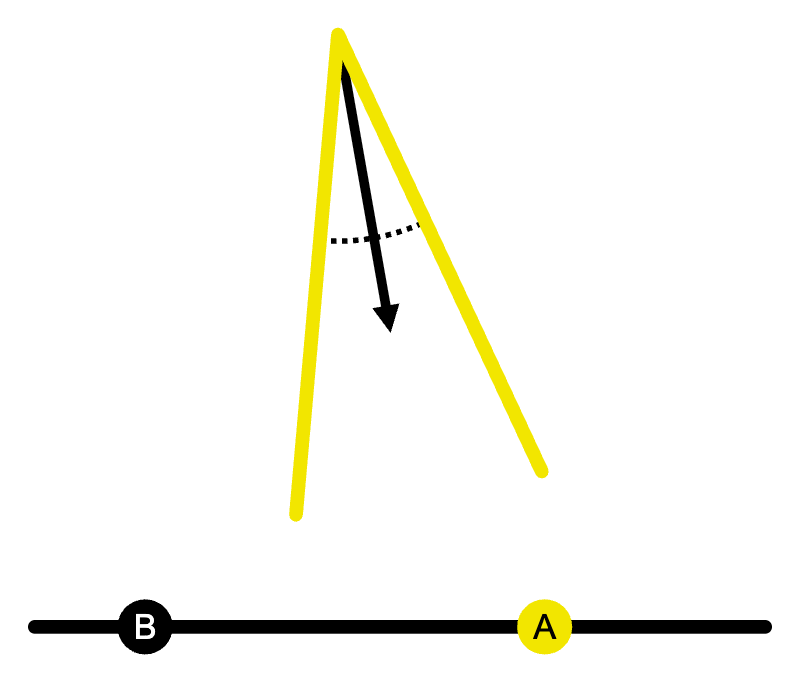
The spot direction and angle are also shown.

One common measure of alignment is the dot product. To measure a fragment's alignment with the cone, its focusedness, we take the dot product between the spot direction and the vector from the light source to fragment. Earlier we computed a vector from the fragment to the light source. Now we need its inverse. Our fragment shader therefore starts off with these assignments:

uniform vec3 spotPositionEye;  // assumed normalized
uniform vec3 spotDirectionEye;
// ...

void main() {
  vec3 lightDirectionEye = normalize(spotDirectionEye - mixPositionEye);
  vec3 fragmentDirectionEye = -lightDirectionEye;
  vec3 focusedness = dot(spotDirectionEye, fragmentDirectionEye);
  // ...
}

uniform vec3 spotPositionEye;  // assumed normalized
uniform vec3 spotDirectionEye;
// ...

void main() {
  vec3 lightDirectionEye = normalize(spotDirectionEye - mixPositionEye);
  vec3 fragmentDirectionEye = -lightDirectionEye;
  vec3 focusedness = dot(spotDirectionEye, fragmentDirectionEye);
  // ...
}

A smooth focusedness value is not quite the measure we want. We want a measure that is 0 when the fragment is outside the cone and 1 when the fragment is inside. Then we could modulate the litness by this value:

float litness = ... * spottedness;

float litness = ... * spottedness;

Perhaps we could compute by the spottedness by writing a conditional statement comparing the focusedness to some threshold like this:

float spottedness;
if (focusedness < cutoff) {
  spottedness = 0;
} else {
  spottedness = 1;
}

float spottedness;
if (focusedness < cutoff) {
  spottedness = 0;
} else {
  spottedness = 1;
}

This logic is already implemented in the GLSL function step. It accepts a threshold and a value to compare against threshold and returns either 0 or 1. We apply a threshold to our focusedness with this call to step:

// ...
uniform float cutoff;

void main() {
  // ...
  let spottedness = step(cutoff, focusedness);
  // ...
}

// ...
uniform float cutoff;

void main() {
  // ...
  let spottedness = step(cutoff, focusedness);
  // ...
}

The cutoff value is the measure of alignment between the cone's edge and the spot direction. We calculate it as the cosine of half the spot angle and upload it as a uniform:

let halfDegrees = spotAngleDegrees * 0.5;
let radians = halfDegrees * Math.PI / 180;
shader.setUniform1f('cutoff', Math.cos(radians));

let halfDegrees = spotAngleDegrees * 0.5;
let radians = halfDegrees * Math.PI / 180;
shader.setUniform1f('cutoff', Math.cos(radians));

Test the spotlight in this renderer, in which you can change the spot angle with the number input and the spot direction by clicking and dragging on the terrain:

The transition between the inside and outside of the cone is immediate, producing an unrealistic hard edge. We expect to see gradual transitions between illumination and shadow. To smooth out the transition, we add a fuzziness parameter that widens the cone. Experiment with increasing the fuzziness in the renderer.

The spot angle establishes the first cone, in which the spottedness is 1. The spot angle plus the fuzziness establishes a second cone. Outside this second cone the spottedness is 0. Between cones, the spottedness runs from 0 to 1 along a continuous cubic function. The GLSL function smoothstep performs this softened thresholding operation. We send it two threshold values:

// ...
uniform float innerCutoff;
uniform float outerCutoff;

void main() {
  // ...
  let spottedness = smoothstep(outerCutoff, innerCutoff, focusedness);
  // ...
}

// ...
uniform float innerCutoff;
uniform float outerCutoff;

void main() {
  // ...
  let spottedness = smoothstep(outerCutoff, innerCutoff, focusedness);
  // ...
}

From TypeScript, we send both cutoffs as uniforms:

let halfDegrees = spotAngleDegrees * 0.5;
let radians = halfDegrees * Math.PI / 180;
shader.setUniform1f('innerCutoff', Math.cos(radians));
radians = (halfDegrees + fuzziness) * Math.PI / 180;
shader.setUniform1f('outerCutoff', Math.cos(radians));

let halfDegrees = spotAngleDegrees * 0.5;
let radians = halfDegrees * Math.PI / 180;
shader.setUniform1f('innerCutoff', Math.cos(radians));
radians = (halfDegrees + fuzziness) * Math.PI / 180;
shader.setUniform1f('outerCutoff', Math.cos(radians));

Spotlights by definition are considered to be near the surfaces they illuminate. A spotlight that is infinitely far away is not really a spotlight. Every fragment would be within its cone, making it a standard directional light.