Sphere Normals

Before you can begin shading, you must define normals across a model's surface. The normal at any given point on the surface points in the direction that the surface faces. For simple shapes, you can reason out what the normals should be. For example, the normals on the right face of a cube point right, and the normals on the top face point up.

The normals for a sphere are also straightforward to calculate. Imagine sending vectors from the sphere's origin to its surface, as shown in this cross section:

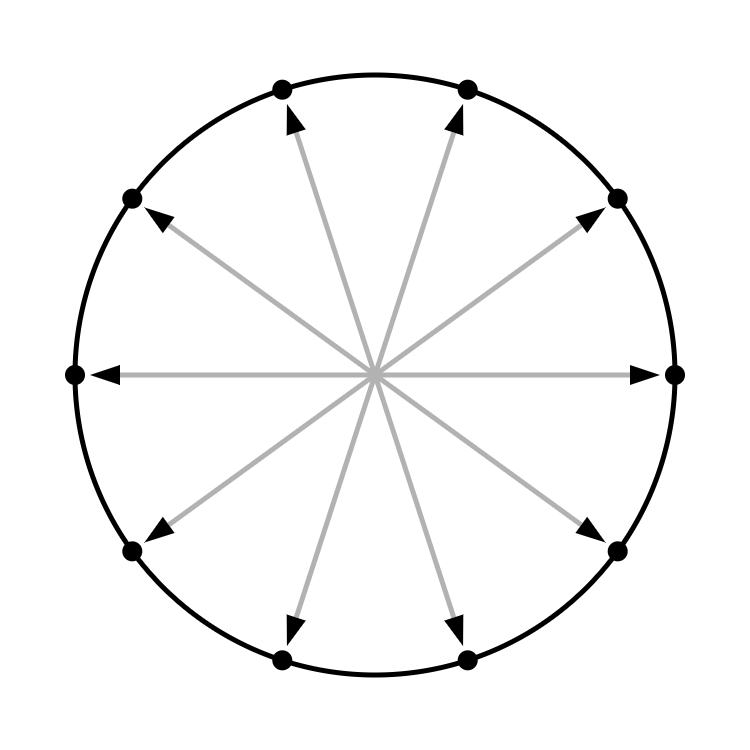
Now imagine extending the vectors out a little further:

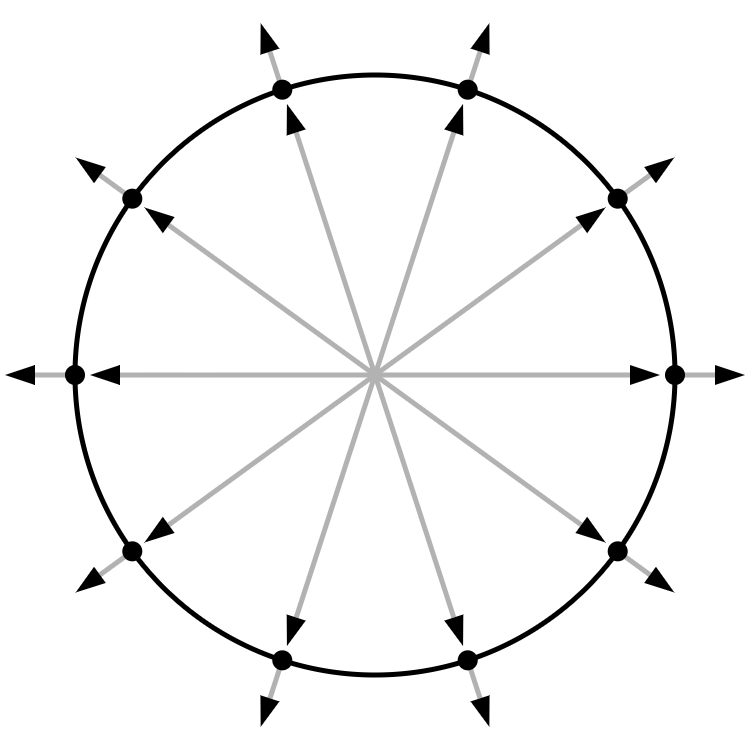
These extensions are perpendicular to the surface, making them normals. They point in the same direction as the position vectors. In fact, if the sphere is centered on the origin, then the position vectors and normal vectors are the same. The only difference is that normals are scaled to have a magnitude of 1 to simplify later calculations.

If you have the position of a sphere's vertex stored in a Vector3 in TypeScript, you can compute the normal with the normalize method you wrote earlier:

content_copynormal = position.normalize();

normal = position.normalize();

Despite their common root, the noun normal and the verb normalize mean different things. To normalize a vector is to scale it to unit length. A normal vector is a vector perpendicular to a surface. Normals also happen to be normalized, but not all normalized vectors are treated as normals.

If you need the normal for a sphere vertex in a GLSL shader, you can compute it from the position with the normalize function, as is done in this vertex shader:

content_copyin vec3 position;
out vec3 mixNormal;

void main() {
  gl_Position = vec4(position, 1.0);
  mixNormal = normalize(position);
}

in vec3 position;
out vec3 mixNormal;

void main() {
  gl_Position = vec4(position, 1.0);
  mixNormal = normalize(position);
}

Here the normal is sent along to the fragment shader. Each fragment will receive an interpolated blend of the surrounding vertex normals. The interpolated normal will be used in the shading calculation.

Explore how the vertex normals influence the shading of a sphere in this renderer:

The sphere is made of relatively few triangles. Yet the surface looks smooth. Uncheck the checkbox to separate the faces. Each quadrilateral is made independent of all others, with its four vertex normals all pointing in the same direction. This polygonal style of rendering was popular in the 1980s and 1990s.